Torque Wrenches and Bicycles

I’ve stated numerous times why torque wrenches are overkill for bikes and that you can pretty much depend on your own judgment as you tighten a bolt. Why? Data. And what follows is rationale for that position. Note that I am not stating that torque wrenches or other preload indicating devices are worthless. Far from it, but it depends on the application, criticality of the interface, and the information at hand. There are some situations where knowing how much preload is in a bolt is vitally important. However, even in those situations, torque wrenches are not the best way to quantify that load.

To understand you must first understand the relation between tightening torque and axial load on the bolt. Perhaps the simplest way to describe it is

T=P*K*D

Where T is the applied torque, P is the load in the bolt, K is what is called a “nut factor”, and D is the bolt diameter. In this equation, it is assumed running torque is equal to zero. Running torque does not add to bolt load. Ever notice how some nuts spin freely on bolts but others take a little effort to turn? The latter case has higher running torque.

In the equation above, K is not a fixed value; it is a function of several things, such as the male to female thread interface, the nut to thread and joint interface, and the head to joint interface. If all surfaces are dry you can get one range of K. Lube just the threads and you will get another. Lube the threads and under the head, you get another. Put Locktite on the threads and you get yet another range. Needless to say, it’s important to understand the physical state (e.g., lubrication) of the joint since for the same torque T, your preload P can be all over the place. In general, as you lube the system, the value of K drops, meaning for the same torque, you get higher preload.

Now in my “real life” as an engineer, I have done torque-tension testing to characterize the range of K for some joints. I collected this data using a calibrated force transducer to measure bolt load and a calibrated torque wrench (I used both a click type and dial type) to apply a specified torque (final torque of 400 lb-in above running torque). My testing was performed with 3/8” NAS bolts, which obviously are much bigger than bolts you find on bicycles, but the fundamental physics holds for smaller bolts. The testing included multiple torque cycles with the bolt in an as-received dry state and also a wet-lubed state. In the aerospace world, we tend to limit the number of times we can re-use a bolt due to uncertainty in the range of K with multiple uses. On bikes, consumers tend to ignore such practices, yet as you will see, doing so can have detrimental effects.

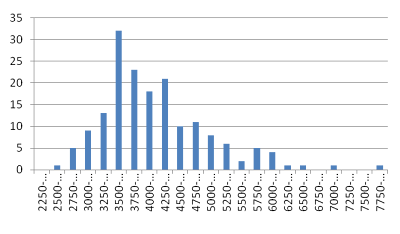
In my first round of testing, from a pool of 10 fasteners I performed 40 torque-tension tests with 4 randomly selected fasteners. After each test I would return the fasteners to the pool and randomly select another 4 for the next test. All bolts were in the unlubed condition. The figure below shows the distribution of bolt load P given the torque T=400 lb-in. The average preload was 4214 lb with a range from 2618 lb to 7760 lb. The 4214 lb average leads to an average nut factor of K=0.253, with a Kmin=0.137 and Kmax=0.407. The distribution plot and the values of Kmin and Kmax clearly show that there is a significant amount of error in preload. With the above values, the preloads are -37.8% and +84.1% from the average preload. That’s some significant error. The high preload values, which are only a couple of samples, could be attributed to something as minimal as body oils contaminating the threads.

I then repeated tests using 6 bolts randomly selected from the pool, and repeated the tests 30 times. During this stage, the preload ranged from 2428 lb to 6482 lb with an average of 3700 lb, leading to K=0.288 and Kmin=0.164 and Kmax=0.439. The min and max preloads were -34.4% to +75.2% from nominal. The important thing here is the increase in average nut factor to 0.288. As more cycles are put on the bolts, wear particles are generated, increasing friction and reducing the efficiency of the bolt/nut. In other words, it now takes more torque to get the desired load.

Next up was a series of 20 tests using 8 randomly selected bolts, but torque was increased to 450 lb-in. The threads were not cleaned, so wear was really an issue. The preload ranged from 2542 lb to 5551 lb with an average of 4040 lb, leading to K=0.297 and Kmin=0.216 and Kmax=0.472. The min and max preloads were -37% to +37.6% from nominal.

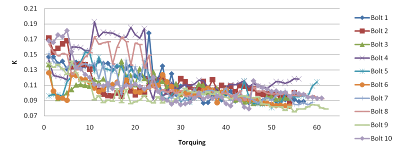
Clearly the number of cycles on the bolt affected the nut factor. Below is a plot of nut factor as a function of torque cycle for each bolt. Two things to take out of this plot are that 1) nut factor increases, and thus bolt preload decreases, with use and 2) for unlubricated bolts the individual K value for a bolt varied widely from one bolt to the next. From a box of 10 bolts, I could randomly select a bolt with a nut factor around K=0.4 while the one next to it may be K=0.2. So, depending on which bolt was picked (and you have no idea of knowing), bolt load could be double or half of desired value.

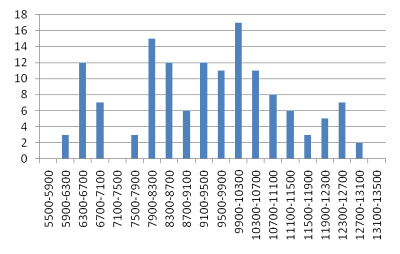
Now when you lubricate bolts, things get quite different. In the first round of testing, I wasn’t completely sure how much lube to apply, so I put just a light coating of wet lube on the threads. I then performed 35 tests with 4 randomly selected bolts from the lot of 10 bolts. The final bolt load distribution had a fairly normal distribution, which was certainly odd, as shown below. This series of tests produced preloads from 5529 lb to 12415 lb with an average of 8988 lb, leading to K=0.119, Kmin=0.086, and Kmax=0.193 and the preload ranging from -38.5% to +38.1% of nominal.

Based on the distribution plot and the wide scatter, I determined I had not apply enough wet lube to the bolt. Adding more lube and performing 30 tests with 6 randomly selected bolts led to the distribution curve below. This series of tests produced preloads from 7901 lb to 13427 lb with an average of 10693 lb, leading to K=0.1, Kmin=0.079, and Kmax=0.135 and the preload ranging from -26.1% to +25.6% of nominal.

Finally I performed another 20 tests with 8 randomly selected bolts, but I reduced the preload to 300 lb-in, in fear of damaging the force transducers. This series of tests produced preloads from 6751 lb to 10620 lb with an average of 8477 lb, leading to K=0.095, Kmin=0.075, and Kmax=0.119 and the preload ranging from -20.4% to +25.3% of nominal.

The graph below shows the individual values of K for each bolt during each torque cycle. The high nut factors from 1-25 cycles is due to the minimal lube applied. The large drop in K is from a liberal application of wet lube. What this graph shows is that 1) lubricating your bolts reduces the effect of “nut factor creep” due to reducing wear particle generation (which is the function of a lubricant) and 2) less scatter from one bolt to the next (indeed, the range of K is very narrow at around K=0.08 to K=0.12).

So what does all this mumbo jumbo mean for our bicycles? Does all this really matter? Well, yes. As an example, one of my bikes is a Specialized Tarmac Pro. The seat tube collar has a single M5 bolt with a torque callout of 55 lb-in. The stem at the steerer tube interface has 4 M4 bolts with a specified torque of 40 lb-in. That’s all the instruction. Even on Specialized’s website, which provides additional installation instructions for the stem, it merely provides the guidance of tightening in a criss-cross pattern at 5 lb-in increments. No mention is made of how clean the thread interface should be, the cleanliness under the bolt head, or what, if any lubrication should be applied. What about running torque? Both of these interfaces clamp carbon parts, so overload is certainly a concern. Let’s take the seat post collar. With T=55 lb-in and D=5 mm (0.19685 in) and a completely unknown K value, just what the heck kind of load can we expect? The testing above indicates K can be anywhere from K=.137 to K=.472, which leads to a clamp load from 592 lb to 2039 lb assuming the 55 lb-in is the effective torque on the bolt. I have no idea what the crush load of my seat post is, but has Specialized designed it for this range? Or suppose I liberally lube the bolt such that now my nut factor may be as low as K=0.075 as the data I collected suggests. This would cause the clamp load to jump to 3725 lb. This load is disconcerting, as even a NAS fastener with strength of 160 ksi would fail in the threaded section with this load. And I doubt Specialized is providing very high strength fasteners (i.e., greater than 160 ksi) with their builds.

Now let’s look at the several fasteners on a bike and address their function and criticality:

Stem to steerer tube – prevent the stem/bars from rotating relative to the wheel by providing enough resistance through friction (clamp force times friction coefficient). A SLIP CRITICAL interface.

Stem to handlebars – we don’t want those bars slipping while riding, so this is another SLIP CRITICAL interface.

Seat post collar – again, we want to avoid the seat slipping on us, so this is another SLIP CRITICAL interface.

Seat rails – what can we say? Another SLIP CRITICAL interface.

Cranks to bottom bracket – we don’t want the cranks from coming loose, and by providing a lot of tension we can reduce the effect of self-loosening. The higher the preload, the less likely we will experience self-loosening, or the number of cycles to loosen will increase. This is a TENSION CRITICAL interface.

Crank ring bolts – these bolts carry shear, but we don’t want them loosening, so this is also a TENSION CRITICAL interface.

Brakes to frame – another TENSION CRITICAL interface since we don’t want the brakes to fall off.

Front derailleur – well, this depends on whether you have a braze-on or clamp on derailleur. For clamp, it’s SLIP CRITICAL, and for braze-on I’d call it a hybrid of SLIP and TENSION CRITICAL.

Rear derailleur – we don’t want the bolt to loosen on us and cause the derailleur to shift outwards, so I’d call this TENSION CRITICAL.

For the tension critical interfaces, we have to further determine if we truly want high preload to maximize fatigue life or merely have a locking feature to hopefully prevent the bolt from coming out. Honestly, all the interfaces I’d classify as the latter. If the interface is metal-on-metal, I’d just apply lube liberally, preload high by feel, and walk away. If it makes you feel better, throw some locktite on the threads. Do note, however, that locktite cures best in a vacuum, and as we don’t have our own vacuum chambers, we may never get a full cure.

For slip critical interfaces, what I’ve always done, particularly with parts I consider as potentially susceptible to crushing, is to keep the bolt as dry as possible, torque a little, try to move the part, and add additional torque as needed to prevent slipping. My goal is to keep K as high as possible to make the efficiency low, giving me lots of error tolerance. And by creeping up I hit the bear minimum needed for my joint functionality. I wouldn’t use a torque wrench because, as already demonstrated, a torque wrench is COMPLETELY WORTHLESS without knowing the nut factor K for the joint. So with absence of vitally important information, I am forced to use my intuition and feel to make a robust joint. My engineering knowledge guides me to abandon my very field and the governing equations because of the lack of design information on the joint.

There are certainly some esoteric reasons for using a torque wrench on your bike. For one, there’s a liability issue. Should you crash due to a failed interface and sue the bike manufacturer, they could ask if a torque wrench was used (although, honestly, given what I have stated above, the torque call-out is ill-defined at best) and that their client is not liable if said wrench was not implemented. Or if you have a warranty claim against the manufacturer, you could bolster your argument by saying you installed per their recommendations, no matter how dubious those recommendations actually were. Though I must say, even if you did use a torque wrench, unless you have verification (e.g., third party watching over you) you may lose that argument. Or you may just want to play with your new toy.

The data is clear – my testing with aerospace grade fasteners, calibrated torque wrenches, and calibrated load transducers shows min and max preload can vary from -38.5% to +84.1% from nominal. If you think that torque wrench is getting you the correct value, think again. That’s a huge error, and I’ve heard about too many broken carbon bits to put my trust into some number stamped on a part with no other information. Remember, T and K are dance partners. T, the number stamped on the part, needs a little more info to meet up with K and waltz off together.

A golden nugget from years ago

There's been a length debate over at www.cyclingforums.com about Powercranks and their effectiveness. What else is new, right? One of the big marketing claims of PCs is that you'll gain a couple of mph in speed which represents "up to 40%" increase in power. The debate has always been how much is merely training effect versus something PCs may actually do. That is, do PCs, as claimed, increase efficiency and then power? Or do they just provide the motivation to train harder and you'd get to the same place with regular cranks? Having used them, I fall into the camp that they don't work magic. If you've peaked on regular cranks, you've peaked. PCs can certainly help you hit your limit just like regular cranks, but they won't push beyond that.

So what did I find in the archives? An old threshold effort from my first month of training with power and in the first 8 months of my bike riding. A little background first:

• I started riding around September 2001
• I crashed in mid Feb 2002 and suffered a broken hip
• Within 3 weeks of the crash I was on an recumbent exercise bike getting my flexibility and moderate strength back
• Within 5-6 weeks of the crash I bought a Computrainer so that I could get back on my real bike and regain full fitness
• Within 4-6 weeks of the crash I bought Joe Friel's cycling book and learned the basic principles of proper training methods

In late April 2002 I did a "40k time trial" on the Computrainer. Looking at the data, I went pretty hard. My heart rate during the effort averaged 157 bpm. That's in the range of my typical HR for an hour effort (155-165 depending on fatigue and/or heat); I've got a slow beating heart. My HR also got up to that level within 2 minutes. These days, after 8+ years of cycling it can take a good 8-10 minutes to reach a steady value. My HR also drops like a rock - 60-80 beats in a minute once the workload is removed.

Now my Computrainer has always read a bit low. The 40k effort was 174 W average on the Computrainer for 77 minutes and 176 W for the first 60 minutes. I have calibrated my Computrainer against a Powertap and the "correct" value for 60 minutes would be 188 W. Fast forward 8 years and my hour power is in the 275-285 W range. So my hour power has increased some 50% through training effect alone. If those Powercranks worked the way they were advertised, I should get another 40% gain for a whopping grand total of 110%!!!!!

Can someone say snake oil?

Stages of friction

There's some renewed talked on the slowtwitch forums about chain lubes and a claim that no lube is just as good as lube. I thought it would be good to provide a brief explanation of friction and wear. Perhaps the easiest way is to show what's going on with the qualitative picture below which is for repeated motion in a single wear track:

When you have fresh surfaces, either with or without lube, stage I exists. Even bare metal-on-metal contact exhibits relatively low friction early on. The duration of stage I is a function of many things, such as the materials, surface coatings, temperature, pressure, atmospheric conditions (air, pure nitrogen, argon, vacuum, etc), and liquid/solid lubricants. As wear particles develop, you enter into stage II. Stage III is a continuation of the wear particle buildup. Eventually, the number of wear particles leaving the wear track is balanced by the particles being generated and you reach a steady-state (stage IV).

The time is takes to go from stage I to stage IV is a function of many things, just like the duration of stage I. It may be anywhere from a single lap to many laps depending on the contact stress, materials, etc.

Some materials may exhibit a decrease in wear as signified by stages V and VI, though without active removal of wear particles, stage IV becomes the dominant player. From my previous entry you can see that for a sample metal-on-metal contact, stage I was short lived and stage II/III was also a short event. The metal pairing reached a steady state level quickly. It should be noted that had I taken a simple brush and wiped the surfaces down to remove the majority of the wear particles, the friction would have temporarily dropped down to stage I levels. Thus, active cleaning is a great way to keep friction low for bare metal-on-metal sliding contact.

In general, liquid lubes will keep the friction down to stage I levels. The lube acts as a transport agent for wear particles. It should be noted that you can still have wear of the materials, and indeed I have tested some VERY expensive grease (as in a few thousand dollars per pound) which continued to wear the surfaces significantly yet kept friction nice and low. However, any lubricant will have a finite life. Starvation occurs eventually and friction jumps up to metal-on-metal steady state levels as shown in Figure 4 of the link above (the June entry).

What does this mean for chains? When you hear that chain squeaking you can be pretty sure you are in stage IV and it's time to clean and relube. The surfaces are lube starved. Can you get a chain to have low friction without lube? Sure. But the chain has to be designed properly. That may mean proper material pairings, an active cleaning process (e.g., a debris wiper), or proper surface treatments (however, you could argue that something like gold plating is actually a form of lubrication).

So remember, it's not about the initial friction but how long the initial friction lasts. If it lasts a short time, then the question becomes how good is the life of my lube if one is used.

PowerCranks – The Final Verdict

My year with PowerCranks (PCs) has come and gone. I received them back in July 2008 and immediately installed them and took them for a spin. Instantly I knew these were something different as I was working muscles not previously stressed in the past despite the tens of thousands of cycling miles on my legs. But would that new pain I was experiencing with these new mechanisms translate into more power on the bike or merely a device for torture?

To answer that question I embarked on a disciplined training regimen of significant riding on the PCs. While I had initially agreed to ride the cranks exclusively, I quickly realized that I wanted to get on the regular cranks at least once a week. This was for several reasons: 1) I could not ride my usual Saturday hard group ride with them and keep up (in other words, those rides would quickly turn to solo endurance rides rather than provide a training stimulus for my VO2 and anaerobic zones), 2) I could not safely ride my group ride with the PCs due to the way they affect both bike handling and remounting (as someone focused on safety this was a big issue for me), and 3) I needed a little variety during the week. So while I did not use them as expected, I feel as though I've been able to assess the cranks and their potential to help riders.

First the facts: I felt I had stagnated in terms of the power I am able to produce. I've got power data going back to before 2003, and over the years that data suggests that I'm topped out in terms of performance. As a time trialist and road racer, my interest lies in aerobic power. As PCs are targeted towards triathletes which are clearly aerobic engines, I thought using them could provide just the right kind of training shakeup to perhaps give me 5 percent or more boost in performance. My workouts were geared towards enhancing aerobic power – a steady mix of tempo, threshold, and VO2 riding.

My best performances of the year were actually in the fall of 2008, within the first few months of using PCs. The graph below shows my normalized power for my time with PCs (red line) and compares against a few key time periods. The green line represents the season prior to using PCs. Do to travel and illness, I just couldn't get very good power down. The black line is an envelope of my all-time best numbers prior to using PCs. A few things to note about this chart: 1) even with a subpar year (the green line) prior to PCs, my power was only 10-15 W lower in the 30-60 minute range, about 4%, 2) my time with PCs shows only a couple of instances where I achieved higher power, and those differences were in the single watt range (i.e., 1-5 W differences), and 3) this graph represents absolute best performances (i.e., cherry picking) rather than repeatable power. This last fact is important. A one-off performance could be due to things like instrumentation error, a new chain, or a newly cleaned chain. More important to me is repeatable power. Nonetheless, the data is what the data is, and while I did set some personal records during my time with PCs, they were not significant in the slightest (1-2% at most). All plotted is my average power. That graph tells much the same story as normalized power.

Looking at a broader set of data, the graphs below show my full set of data for 2003 to present. You may notice that 2003 and 2004 were clearly the low points in my cycling. Those were the initial years of my serious cycling and I would expect those points to be the low hanging fruit. If you neglect those first 2 years you can see how tightly bundled all these data are.

But like I said, I care more about repeatable power rather than one-off performances. I want to know what I can expect to bring come race day. In that vain, I took all my daily power data and found the best performances. I averaged these top performances to come up with power numbers I could bank on. The plot below takes the average of my top 20 performances for times from 10 minutes to 60 minutes. What we see is the 2008 was clearly an aberration. It sticks out as being a below par year, yet even 2008 was not that bad. Power at any duration was no worse than 7-8 W. In other words, even though it was lousy in terms of absolute power, my repeatable power was actually quite good.

Of course, the careful reader may wonder about taking 20 rides and averaging them. That's a legitimate concern, and to mitigate that concern somewhat, we can compare 20 rides to 10 rides and also the peak values. The plot below for 2009 shows only a 1-2 W difference between 10 and 20 rides, and only a 5-10 W difference between absolute peak and a 10 ride average. The same can be seen for the 2007 data.

So if I look at all this data objectively, I would conclude that for me, PowerCranks did not positively affect my long-term power (that being 20 minutes or longer). The data collected indicates that my power numbers were within the norms of prior years, and any perceived increase in power was within the stated error of the measurement device itself (a Saris Powertap).

Now the manufacturer of PCs will counter that an inability to show an increase could be due to a few things: 1) I did not ride the PCs exclusively or 2) my stroke was already good and PCs would not be able to help further.

The first point is factually accurate. As already mentioned I did not use the PCs exclusively. However, PC use did account for over 50% of my training time over the last year (which in total was nearly 500 hours). I would have used them more but I experienced some injuries associated with the comination of the PCs and the Time ATAC pedals. I was getting tendonitis-like pain in my left ankle only when using PCs. I stopped using them for several weeks to heal. Upon returning to them, the ankle pain came back, though my hip flexors were ready for long rides with the PCs. Subjectively, I felt I was adapted to them within 2 months of use. I got to the point were I could ride for 3-4 hours with no pain and while sustaining my overall power. Since the manufacturer of PCs can not provide an objective way to determine adaptation, all we are left with is subjective reporting, and my subjective interpretation is that I was indeed adapted.

Regarding the second point, that is something we may never know. However, I do feel my stroke is pretty good. I live in the Houston, Texas area, which is pancake flat. My specific area has long, uninterrupted flat roads with a coastal breeze in the warmer months and consistent cold north wind in the winter. The terrain does not allow for much variable power. You just sit on the bike and grind away. I've got well over 70,000 miles of this riding in my legs.

So perhaps I'm just the exception and a genetic freak who has a perfect spin already. Or perhaps too much is made of unweighting on the upstroke. To this end, I sought out some actually pedal force data. Unfortunately there isn't very much pedal force data out there, but the exception is the work of Kautz, et. al. In “The Pedaling Technique of Elite Endurance Cyclists: Changes with Increasing Workload at Constant Cadence” Kautz and his colleagues measured pedal force data of category 1 and 2 riders. The study was performed many year before things like PCs, Rotorcranks, or elliptical chainrings hit their stride, and on a positive note the raw data is available on the internet. An example of some of this data is shown below, which is for the rider with the “worst” pedal stroke. The blue line shows the force tangential to the crank. You can see that after the rider passes the 6 o'clock position his stroke becomes “inefficient” as negative torque is applied, as indicated by the greenish line.

We can examine the normalized pedal force for all subjects in the plot below. In this graph, tangential pedal forces for each rider are divided by the peak tangential force for the rider. The dashed red lines indicate the absolute min and max values. Error bars in blue somewhat mask the average for the entire data set, but it can be seen that the overall average of the many subjects is positive through the entire stroke. In other words, riders tend to naturally generate a good stroke.

But what if the rider with the “lousy” stroke used PCs to get rid of that negative torque. The manufacturer has made claims on the internet that PCs force the rider to “unweight and nothing more”. So if we analytically remove negative torque from the riders we get an estimate of the potential increase in power due to that “perfect” pedal stroke. The results are rather surprising. The objective raw data would indicate the following improvements: 8.08%, 4.28%, 4.13%, 4%, 3.64%, 2.61%, 2.15%, 2%, 1.84%, 1.29%, 1.07%, 0.99%, 0.47%, 0.32%, 0.17%, 0.07%, 0.01%, and 4 riders at 0%. The average improvement for this set of riders is a whopping 1.77%. To put this in perspective, that's about 5 W on a 300 W threshold.

So clearly there's the potential (albeit not much based on the Kautz data) for improved pedal technique, but can PCs actually deliver that improvement? The figure below is from the manufacturer and shows a single user on PCs and regular cranks. The user switches between the cranks and force data is recorded. What we see is the PC data shows no negative pedal forces (as it shouldn't), yet this PC rider produces negative force when using regular cranks. I contend that if this PC rider trains from birth to death with PCs, he will likely never generate a force distribution on regular cranks that mimics PCs. Why? One can never develop perfectly coordinate pedal motion. Because fixed cranks are, well, fixed, all the pistons would have to be firing EXACTLY 180 degrees out of phase. I feel I'm pretty coordinated, yet even I know I can't get 180 degrees exactly. The slight phase shift means at some point my downward moving leg will be assisting my upward moving leg. This assistance will always cause the force distribution to deviate away from the PC force distribution. That's simple mechanics.

So is it all bad news for PCs? Are they nothing but a bunch of hogwash? Well, in my opinion yes and no. They are not some sort of magic bullet which allows you to take something from nothing. If you are at your physiological limit on regular cranks PCs, in my opinion, will not improve your power further.

But there's the rub – how to do you know when you are at your physiological limit? Unless you have many years of power data it's hard to know. After using PCs, I do feel they can aid a rider in developing their power. For riders that are still improving, PCs provide additional difficulty that could help them raise their pain thresholds and improve their power. Thus, I see them as more a mental tool rather than a physical one. Do I think you can get the same improvements without them? You bet. But for those riders that need a little nudging, they make work.

And so ends the PC experiment. My n=1 experience tells me they are as effective as a placebo solution at raising my power. They did nothing for my power. The interesting thing will be this fall when I get back in the full swing of more intense training. Due to a late May crash, my summer season was a washout, and I've had difficulty getting my power back in the oppressive heat (worst summer in decades). So the question will be can I return to the same form using regular cranks that I had last fall on PowerCranks? My bet is yes...

Post-crash 1 month

Between crash recovery and the heat, my power is still way down. I finally took the time to see just how pathetic things have been of late. Below is a plot of normalized power. Across the board I'm down about 20% compared to the best values over the last 10 months. I'm also down 10-20% compared to the month before the crash. My month prior is showing a little dip in power, perhaps due to the onset of the summer time heat.

The good news is I'm back to doing threshold work and I'm just about pain free. The bad news is I've got a long way to go before my power is back where it should be. I'm thinking I'll be able to make some good gains this week and pop that bottom curve up quite a bit. We shall see...

Back in the saddle again...

Slowly getting back into riding after 2+ weeks off the bike due to my crash. Fitness has gone to pot and it's gotten a LOT hotter since the crash. A double whammy. Trying to come back in 100+ degree heat is not easy. Per my plan, I came back on regular cranks. I had a major groin injury where sometimes it would hurt to simply apply significant pressure on the pedals. By riding regular cranks I could help the weak leg around if need be.

That said, today (25 June) was my first ride on PCs in nearly a month. 2 1/2 weeks down, a week and a half of regular cranks, and now the Powercranks. So common wisdom would tell you I'd be detrained, right? I mean 2.5 weeks of zero exercise and 4 weeks total of no PC riding. Nope. Legs were perfectly coordinated and absolutely no fatigue in a 90 minute ride this afternoon. Fortunately storms pushed through to drop the temps down to a manageable level or else I wouldn't have lasted 90 minutes. Not for lack of PC fitness but heat related fatigue. I'll say that 90 minutes with no issues is proof positive of PC adaptation, but I know there are some out there who won't have any of it.

Not riding PCs for the last week+ was the right move, and at the same time I confirmed that I was again reminded how PC riding is not the same thing as one-legged drills on fixed cranks. On the way home as I rolled up to my house I was doing some single leg spinning with the PCs. Instantly when I started on the injured leg (about 95% recovered thankfully) I got instant pain. I'd just ridden 90 minutes pain free and the first stroke one-legged sent me cringing. It just goes to show that completely different motions are involved when pedaling with one leg versus pedaling with two legs, even when the cranks are decoupled.

But physics aside, it's coming to the end of the PC use. According to my records, next week will have been one year since I received them in the mail. The data I've collected has shown some things, and it will be compiled and put into one last PC report for the world to see.

Stay tuned

Crash Recovery

It's been a rough week. The crash I had last Saturday did a lot more damage than I expected. Sunday I just hung out at home, barely able to move at times. Sleeping was a pain. Monday and Tuesday I stayed home from work for fear of moving around too much. Tuesday afternoon I "manned up" and went out for a ride. What a mistake that was. I was barely able to get my leg over the top tube before the ride. The ride itself was incredibly painful. I'd get a pain on the inside of my thigh that would shoot down to the outside of my knee, almost like my sciatic nerve was getting twinged. I could manage only 30 minutes of riding at a whopping 90 W. And that was pushing it! I guess I have to reset my functional threshold down a good 50-60%...

Wednesday was the first day to go back to work, which I did on crutches. I could not walk more than a hundred yards or so before the pain really set in. Plus it saved me from having to look like an animal when I walked. My wife was affectionately calling me "Cornelius" as I walked with an ape-like gait. Thanks.

Thursday was another day at home, too sore from moving around too much Wednesday. By Friday I was starting to feel better, though I still walked like an inhabitant of Planet of the Apes, but of the same kind as Charlton Heston or Mark Wahlberg...

Was forbidden from riding over the weekend, but by Sunday night I'm thinking I may try to sneak in a ride early this week. I still can't walk perfectly, and if I lay on my side I can not perform a side leg lift of my left leg. It's going to take some time to recover from this crash.

On the plus side, I made a freaking good chocolate sorbetto. Whenever I'm in Turin I go to Grom Gelateria (best gelato in the world IMO). The have a ciocolato extra noir sorbetto that knocks your socks off. I pretty much recreated it Sunday. The stuff is deadly.